Pseudospectral optimal control
Pseudospectral optimal control is a computational method for solving optimal control problems. Pseudospectral (PS) optimal control techniques have been extensively used to solve a wide range of problems such as those arising in UAV trajectory generation, missile guidance, control of robotic arms, vibration damping, lunar guidance, magnetic control, swing-up and stabilization of an inverted pendulum, orbit transfers, tether libration control, and ascent guidance.[1]
Contents |
Overview
Solving an optimal control problem requires the approximation of three types of mathematical objects: the integration in the cost function, the differential equation of the control system, and the state-control constraints. An ideal approximation method should be efficient for all three approximation tasks. A method that is efficient for one of them, for instance an efficient ODE solver, may not be an efficient method for the other two objects. These requirements make PS methods ideal because they are efficient for the approximation of all three mathematical objects as proved in,[2][3] and.[4] In a pseudospectral method, the continuous functions are approximated at a set of carefully selected quadrature nodes. The quadrature nodes are determined by the corresponding orthogonal polynomial basis used for the approximation. In PS optimal control, Legendre and Chebyshev polynomials are commonly used. Mathematically, quadrature nodes are able to achieve high accuracy with few number of points. For instance, the interpolating polynomial of any smooth function (C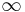 ) at Legendre–Gauss–Lobatto nodes converges in L2 sense at the so-called spectral rate, i.e., faster than any polynomial rate.[3]
) at Legendre–Gauss–Lobatto nodes converges in L2 sense at the so-called spectral rate, i.e., faster than any polynomial rate.[3]
Details
These methods include forms of the collocation at Legendre–Gauss–Lobatto points,[2][5][6][7] collocation at Chebyshev–Gauss–Lobatto points,[8][9] Legendre–Gauss points[10][11][12][13] (known as the Gauss Pseudospectral Method), and collocation at Legendre–Gauss–Radau points[14] (known as the Radau Pseudospectral Method). It is also noted that versions of the Gauss and Radau pseudospectral methods have been developed for solving infinite-horizon optimal control problems.[15] It is important to note that the Lobatto pseudospectral method has the property that the differentiation matrix is square and singular whereas the Gauss and Radau pseudospectral methods have the property that the differentiation matrices are non-square and full rank. This last property of the Gauss and Radau pseudospectral methods leads to the fact that either of these latter two methods can be written equivalently in either differential or implicit integral form.[16]
In pseudospectral methods, integration is approximated by quadrature rules, which provide the best numerical integration result. For example, with just N nodes, a Legendre-Gauss quadrature integration achieves zero error for any polynomial integrand of degree less than or equal to 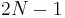 . In the PS discretization of the ODE involved in optimal control problems, a simple but highly accurate differentiation matrix is used for the derivatives. Because a PS method enforces the system at the selected nodes, the state-control constraints can be discretized straightforwardly. All these mathematical advantages make pseudospectral methods a straightforward discretization tool for continuous optimal control problems. One interesting property of pseudospectral optimal control is that, if done correctly, it permits commutativity between discretization and dualization. Specifically, this commutativity exists if the Gauss pseudospectral method[10] (GPM, which uses Legendre–Gauss points) or the Radau pseudospectral method[14] (RPM, which uses Legendre–Gauss–Radau points) are used. For either the GPM or RPM, the KKT multipliers are related to the costates of the continuous problem in an algebraically simple manner.[10][14] In the case of Gauss-Lobatto points, this commutativity is lost because the transformed adjoint system is singular in the discretized costate.[16]
. In the PS discretization of the ODE involved in optimal control problems, a simple but highly accurate differentiation matrix is used for the derivatives. Because a PS method enforces the system at the selected nodes, the state-control constraints can be discretized straightforwardly. All these mathematical advantages make pseudospectral methods a straightforward discretization tool for continuous optimal control problems. One interesting property of pseudospectral optimal control is that, if done correctly, it permits commutativity between discretization and dualization. Specifically, this commutativity exists if the Gauss pseudospectral method[10] (GPM, which uses Legendre–Gauss points) or the Radau pseudospectral method[14] (RPM, which uses Legendre–Gauss–Radau points) are used. For either the GPM or RPM, the KKT multipliers are related to the costates of the continuous problem in an algebraically simple manner.[10][14] In the case of Gauss-Lobatto points, this commutativity is lost because the transformed adjoint system is singular in the discretized costate.[16]
References
- ^ Q. Gong, W. Kang, N. Bedrossian, F. Fahroo, P. Sekhavat and K. Bollino, Pseudospectral Optimal Control for Military and Industrial Applications, 46th IEEE Conference on Decision and Control, New Orleans, LA, pp. 4128-4142, Dec. 2007.
- ^ a b Q. Gong, W. Kang and I. M. Ross, A Pseudospectral Method for The Optimal Control of Constrained Feedback Linearizable Systems, IEEE Trans. Auto. Cont., Vol.~51, No.~7, July 2006, pp.~1115–1129.
- ^ a b J. S. Hesthaven, S. Gottlieb and D. Gottlieb, Spectral methods for time-dependent problems, Cambridge University Press, 2007. ISBN 9780521792110
- ^ Q. Gong, I. M. Ross, W. Kang and Fahroo, F., Connections between the covector mapping theorem and convergence of pseudospectral methods for optimal control, Computational Optimization and Applications, Springer Netherlands, published online: 31 October 2007, to appear in Journal, 2008.
- ^ Elnagar, J., Kazemi, M. A. and Razzaghi, M., The Pseudospectral Legendre Method for Discretizing Optimal Control Problems, IEEE Transactions on Automatic Control, Vol. 40, No. 10, 1995, pp. 1793–1796
- ^ F. Fahroo and I. M. Ross, Costate Estimation by a Legendre Pseudospectral Method, Journal of Guidance, Control and Dynamics, Vol.24, No.2, March–April 2001, pp.270–277.
- ^ Gong, Q., Fahroo, F., and Ross, I.M., "Spectral Algorithm for Pseudospectral Methods in Optimal Control," "Journal of Guidance, Control, and Dynamics," Vol. 31, No. 3, 2008.
- ^ Elnagar, G. and Kazemi, "Pseudospectral Chebyshev Optimal Control of Constrained Nonlinear Dynamical Systems," Computational Optimization and Applications, Vol. 17, No. 2, pp. 195–217
- ^ Fahroo, F., and Ross, I. M., "Direct Trajectory Optimization via a Chebyshev Pseudospectral Method," Journal of Guidance, Control, and Dynamics, Vol. 25, pp. 160–166
- ^ a b c Benson, D. A., Huntington, G. T., Thorvaldsen, T. P., and Rao, A. V., "Direct Trajectory Optimization and Costate Estimation via an Orthogonal Collocation Method," Journal of Guidance, Control and Dynamics, Vol. 29, No. 6, November–December, 2006, pp. 1435–1440
- ^ Benson, D. A., A Gauss Pseudospectral Transcription for Optimal Control, Ph.D. Thesis, Dept. of Aeronautics and Astronautics, Massachusetts Institute of Technology, November 2004. http://dspace.mit.edu/handle/1721.1/28919
- ^ Huntington, G. T., Advancement and Analysis of a Gauss Pseudospectral Transcription for Optimal Control, Ph.D. Thesis, Dept. of Aeronautics and Astronautics, Massachusetts Institute of Technology, May 2007. http://dspace.mit.edu/handle/1721.1/42180
- ^ Rao, A. V., Benson, D. A., Darby, C. L., Patterson, M. A., Francolin, C., Sanders, I., and Huntington, G. T., "Algorithm 902: GPOPS, A Matlab Software for Solving Multiple-Phase Optimal Control Problems Using the Gauss Pseudospectral Method, ACM Transactions on Mathematical Software, Vol. 37, No. 2, April–June, 2010, Article 22, pages 22:1-22:39.
- ^ a b c Garg, D. A., Patterson, M. A., Darby, C. L., Francolin, C., Huntington, G. T., Hager, W. W., and Rao, A. V., "Direct Trajectory Optimization and Costate Estimation of Finite-Horizon and Infinite-Horizon Optimal Control Problems Using a Radau Pseudospectral Method," Computational Optimization and Applications, Vol., 49, No. 2, June 2011, pp. 335-358.
- ^ Garg, D. A., Hager, W. W., and Rao, A. V., "Pseudospectral Methods for Solving Infinite-Horizon Optimal Control Problems," Automatica, Vol. 47, No. 4, April 2011, pp. 829-837.
- ^ a b Garg. D., Patterson, M. A., Hager, W. W., Rao, A. V., Benson, D. A., and Huntington, G. T., "A Unified Framework for the Numerical Solution of Optimal Control Problems Using Pseudospectral Methods, Automatica, Vol. 46, No. 11, November 2010, pp. 1843-1851.
Further reading
- GPOPS, General Pseudospectral Optimal Control Software. http://www.gpops.org.